This sixth article of the mathematical journey through open source, introduces you to the imaginary numbers through octave.

<< Fifth Article

Yes, we have done the powerful matrix math with octave, without even thinking of how it is internally done. Now, on the same note, let’s continue to explore one of the most fascinating or rather most imaginary stuff of math.

i Fun

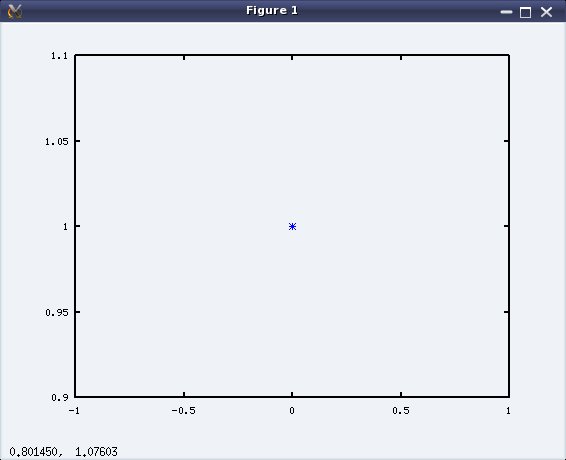
Yes what else the imaginary numbers, numbers which really don’t exist but we try to visualize them as points on a 2-D plane with the real part on x-axis and the imaginary part on y-axis. So to plot the imaginary i, with a blue star (*), issue the following command at the octave prompt:

$ octave -qf
octave:1> plot(i, "b*")
octave:2>

and here pops the display window as shown in Figure 3.

Figure 3: Plot of i (sqrt(-1))

What is this i? Just square root of -1. Simple! Right? Remember, we got an error trying sqrt(-1) in bc. octave is neat. It will answer you politely with an i. Still confused. Just check out the following:

$ octave -qf
octave:1> i
ans =  0 + 1i
octave:2> i * i
ans = -1
octave:3> sqrt(-1)
ans =  0 + 1i
octave:4> i^3
ans = -0 - 1i
octave:5>

i Puzzle

And now comes the puzzle part. What is the imaginary part of iⁱ? It’s zero. What? Is it a real number? Yes it is. It is in fact equal to e^-π/2. Check out for yourself:

$ octave -qf
octave:1> i^i
ans =  0.20788
octave:2> exp(-pi/2)
ans =  0.20788
octave:3> 

Yes, you don’t really need to bother about how. octave just gets you there. And that’s fun with mathematics without getting into mathematics.

i: just a number

If you are not puzzled by this, great! In fact, as the imaginary numbers are numbers, just special numbers, in octave, they can be used in any operations you may think of with numbers. Try out sqrt, exp, log – addition, subtraction, multiplication, division are just trivial ones. And more fun would be with the octave power of vectors & matrices. Watch out:

$ octave -qf
octave:1> sqrt(i)
ans =  0.70711 + 0.70711i
octave:2> exp(i)
ans =  0.54030 + 0.84147i
octave:3> log(i)
ans =  0.00000 + 1.57080i
octave:4>  [i  # Press <Enter> here
>           i] * [i i]
ans =

  -1  -1
  -1  -1

octave:5>

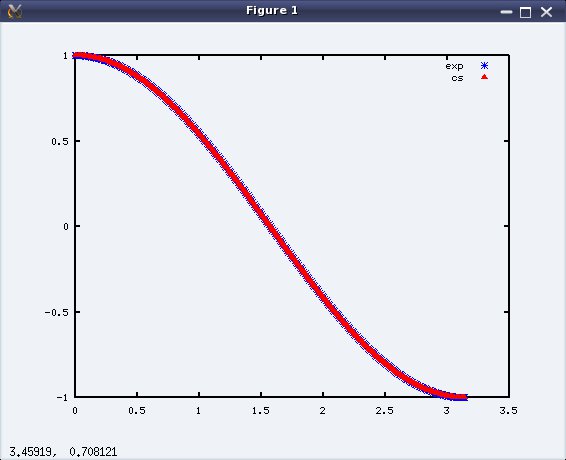
Is e^iθ really cos θ + i sin θ?

A very simple check. Let’s plot both the curves. Let θ (theta) be set to values from 0 to π (pi) with say intervals of 0.01, and then let’s plot the two curves in blue and red:

$ octave -qf
octave:1> th=0:0.01:pi;
octave:2> plot(th, exp(i*th), "b*;exp;", th, cos(th)+i*sin(th), "r^;cs;")
octave:3> 

Figure 4 shows the plot with the 2 curves coinciding exactly with each other.

Figure 4: Plot of Euler’s equality

Equipped with i, let’s play out with more puzzles, as we move on. Get ready with octave controls.

Seventh Article >>

Anil Kumar Pugalia (123 Posts)

The author is a hobbyist in open source hardware and software, with a passion for mathematics, and philosopher in thoughts. A gold medallist from the Indian Institute of Science, Linux, mathematics and knowledge sharing are few of his passions. He experiments with Linux and embedded systems to share his learnings through his weekend workshops. Learn more about him and his experiments at https://sysplay.in.

   Send article as PDF