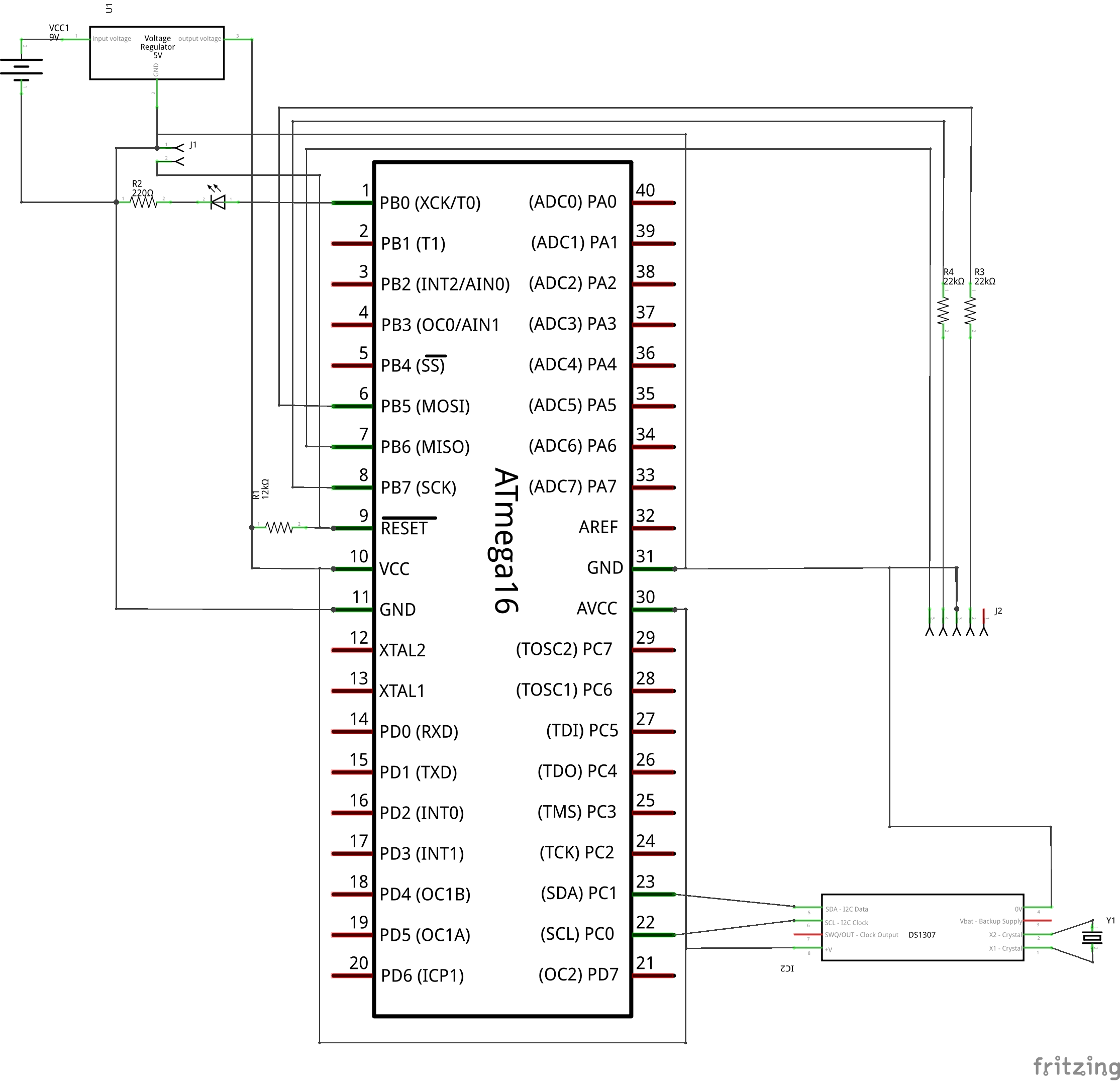
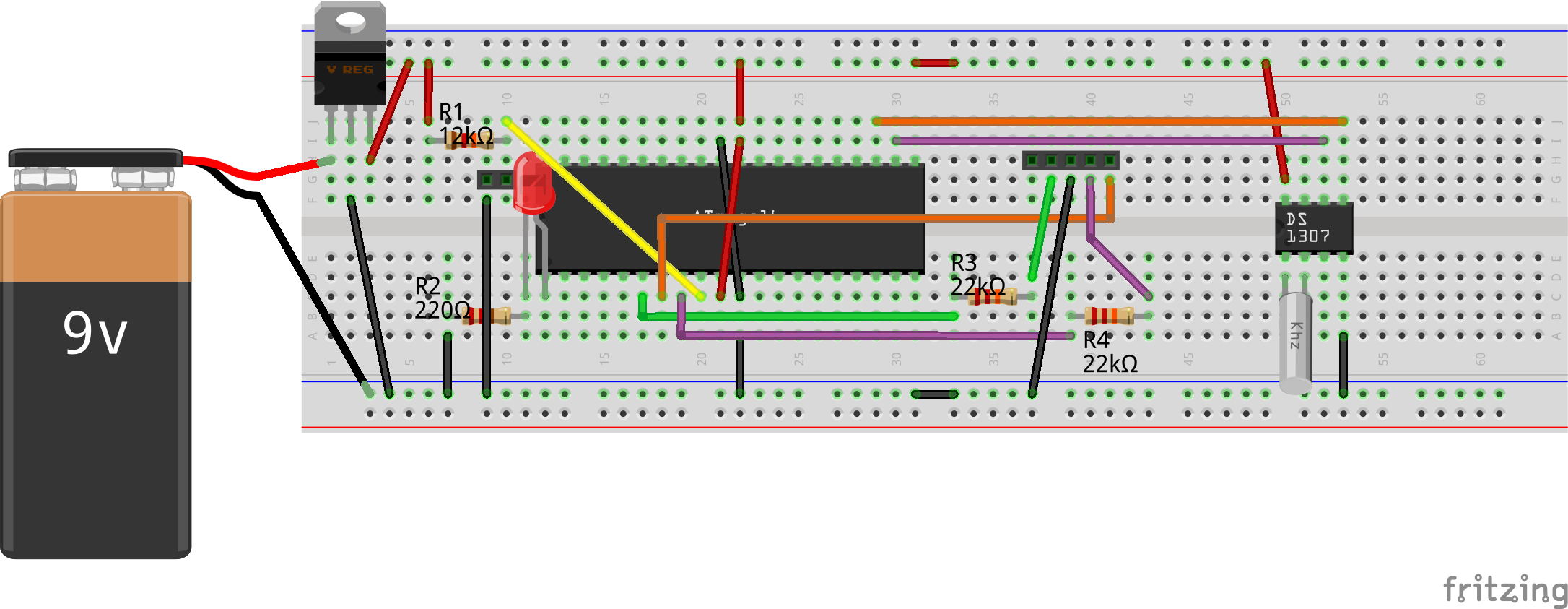
This 17th article in the series of “Do It Yourself: Electronics”, demonstrates generating various waveforms, using the AVR micro-controller ATmega16.
<< Previous Article
Immediately after Pugs generated the 1KHz sine wave, he got the idea of generating other interesting waveforms like triangular and ramp. So, before trying some resistor-capacitor (RC) based experiments in his room, as per his plan, he first thought of just doing some more experiments with the waveforms, using his micro-controller ATmega16.
On little analysis of his code from the previous article, he realized the following:
- He doesn’t really need to ride these waveforms on a centred DC voltage like the sine wave
- And there needs to be a corresponding array containing the amplitudes for each of the waveforms
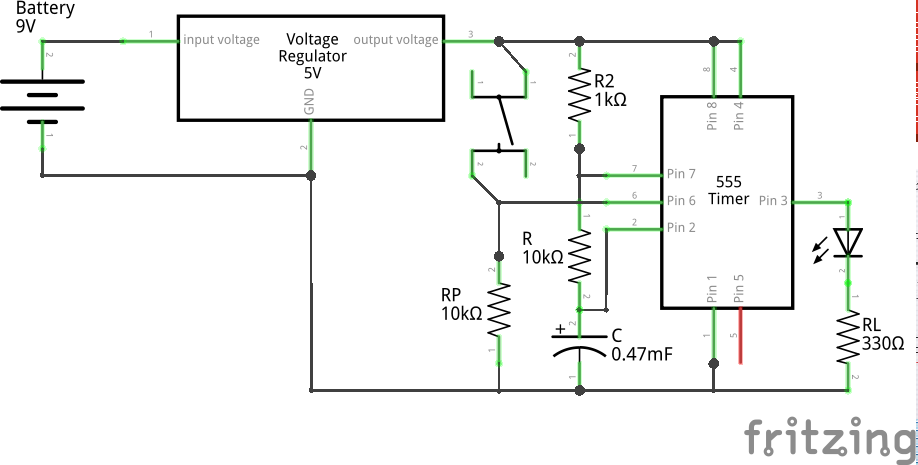
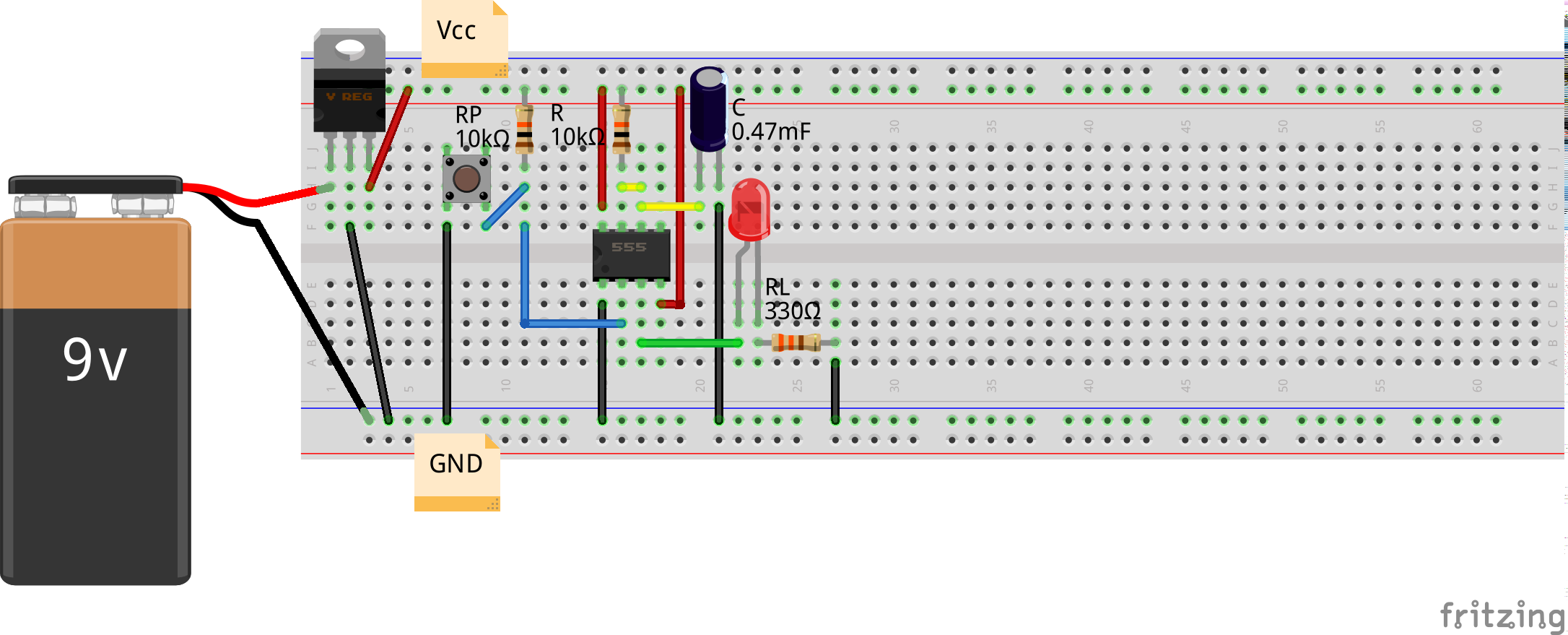
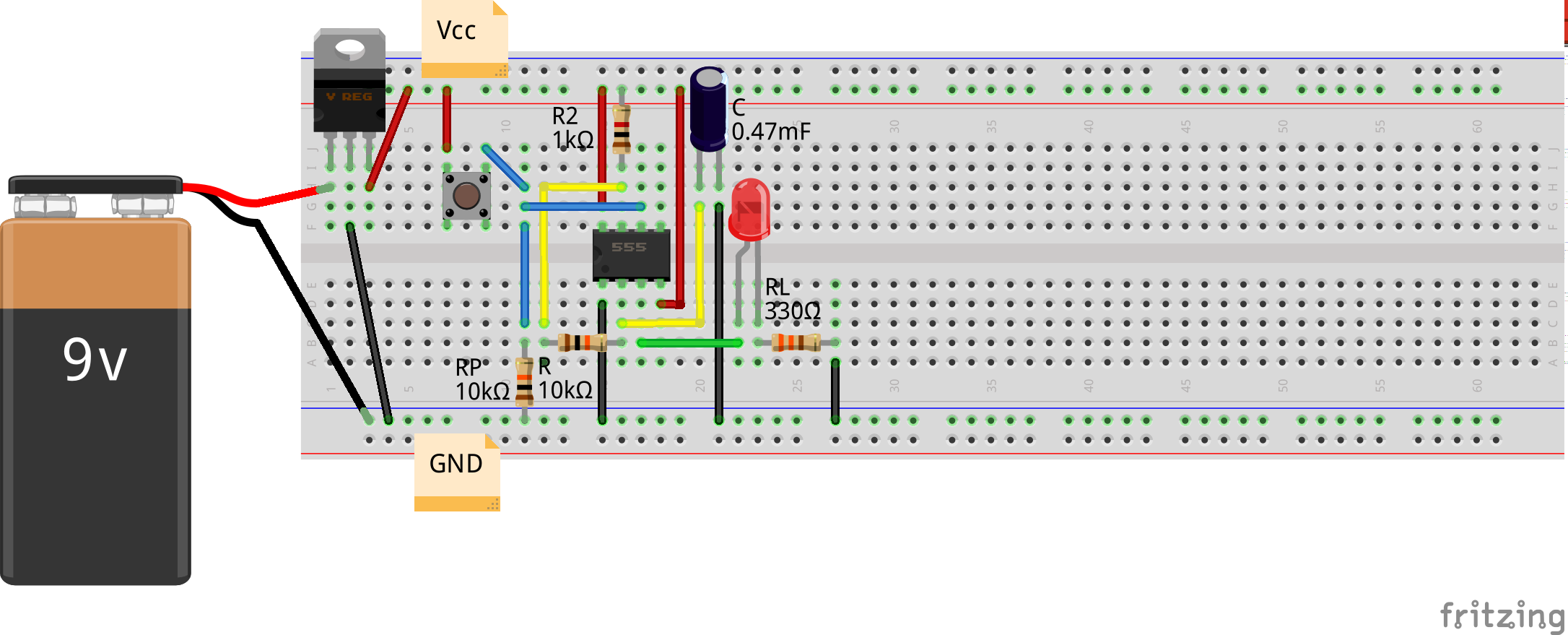
With that, he got an idea of run-time switching between the different waveforms, on say a switch press. And hence he connected a small switch to pin PB2, with its other end grounded, which he initialized to be pulled-up in the code as follows:
void init_switch(void)
{
DDRB &= ~0b00000100; // PB2 as input
PORTB |= 0b00000100; // Pull up on PB2
}
Now for dynamic switching, Pugs modified the function set_amplitude_centred() to work with all waveforms by taking an additional centred voltage parameter. Also, he defined an additional waveform array to contain the various waveform amplitude arrays, as follows(, so as to be able to switch between them, based on the switch press):
struct
{
int dc_off;
int cnt;
int *amp;
} waveform[] =
{
{DC_OFF, ARR_SIZE(sine), sine},
{0, ARR_SIZE(tri_1k), tri_1k},
{0, ARR_SIZE(tri_2k), tri_2k},
{0, ARR_SIZE(ramp_1k), ramp_1k},
{0, ARR_SIZE(ramp_2k), ramp_2k}
};
where sine, tri_1k, tri_2k, ramp_1k, ramp_2k are the various waveform amplitude arrays defined as follows (assuming the same interrupt cycle of 50us):
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
// 0, 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, 198, 216, 234, 252, 270, 288, 306,
// 324, 342 degrees
int sine[] = {0, 3, 6, 8, 9, 10, 9, 8, 6, 3, 0, -3, -6, -8, -9, -10, -9, -8, -6, -3};
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
int tri_1k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
/* Length = l = 10. Period = l * 50us = 500us = 0.5ms. f = 2KHz */
int tri_2k[] = {0, 2, 4, 6, 8, 10, 8, 6, 4, 2};
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
int ramp_1k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
};
/* Length = l = 10. Period = l * 50us = 500us = 0.5ms. f = 2KHz */
int ramp_2k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
With all the infrastructure set, Pugs added the variable cur_wave_i for indexing the current waveform and globalized the variable i – the index into the individual amplitude arrays from the interrupt handler aka ISR. Here’s the modified switching logic in the interrupt handler:
int cur_wave_i = 0;
int i = 0;
...
ISR(TIMER0_COMP_vect)
{
set_amplitude_centred(waveform[cur_wave_i].dc_off,
AMP_FACTOR * waveform[cur_wave_i].amp[i]);
if (++i == waveform[cur_wave_i].cnt)
i = 0;
}
Note that, cur_wave_i needs to be global as would be updated from the main() based on the switch press but why has been i globalized? Think harder. And you’d realize that, as the amplitude arrays are of different sizes, the value of i could become out of array size, during switching of the array to be used on switch press. Hence, it also needs to be reset to 0, during the update of cur_wave_i. With all these changes in the previous article’s sine_wave.c code, here’s the final code as waveforms.c:
/*
* Generates variety of waveforms on OC2/PD7, using PWM on Timer 2.
* Variety is generated one at a time, changing based on switch press
* connected to PB2.
*
* The timing is achieved using timer interrupt handler of Timer 0 triggering
* at a 20KHz frequency, i.e. every 50us.
*/
#include <avr/io.h>
#include <avr/interrupt.h>
#include <util/delay.h>
#define ARR_SIZE(a) (sizeof(a) / sizeof(*a))
#define PRESCALAR_BITS 0b010
#define PRESCALAR 8 // Gives 1MHz clock
#define DC_OFF 127 // Centered
#define AMP_FACTOR 5 // Should range from 1-12, for 8-bit values between 0 & 2*12*10
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
// 0, 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, 198, 216, 234, 252, 270, 288, 306,
// 324, 342 degrees
int sine[] = {0, 3, 6, 8, 9, 10, 9, 8, 6, 3, 0, -3, -6, -8, -9, -10, -9, -8, -6, -3};
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
int tri_1k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
/* Length = l = 10. Period = l * 50us = 500us = 0.5ms. f = 2KHz */
int tri_2k[] = {0, 2, 4, 6, 8, 10, 8, 6, 4, 2};
/* Length = l = 20. Period = l * 50us = 1000us = 1ms. f = 1KHz */
int ramp_1k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
};
/* Length = l = 10. Period = l * 50us = 500us = 0.5ms. f = 2KHz */
int ramp_2k[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
struct
{
int dc_off;
int cnt;
int *amp;
} waveform[] =
{
{DC_OFF, ARR_SIZE(sine), sine},
{0, ARR_SIZE(tri_1k), tri_1k},
{0, ARR_SIZE(tri_2k), tri_2k},
{0, ARR_SIZE(ramp_1k), ramp_1k},
{0, ARR_SIZE(ramp_2k), ramp_2k}
};
int cur_wave_i = 0;
int i = 0;
void set_amplitude_centred(uint8_t centre, uint8_t a)
{
OCR2 = (centre + a);
}
ISR(TIMER0_COMP_vect)
{
set_amplitude_centred(waveform[cur_wave_i].dc_off,
AMP_FACTOR * waveform[cur_wave_i].amp[i]);
if (++i == waveform[cur_wave_i].cnt)
i = 0;
}
void init_pwm(void)
{
DDRD |= 0b10000000; // PD7
OCR2 = 0; // Initialize to 0V output
// Setup OC2 on PD7
TCCR2 = (1 << WGM21) | (1 << WGM20); /* Fast PWM */
TCCR2 |= (2 << COM20); /* Clear on Match */
TCCR2 |= (1 << CS20); /* No prescaling => Clock @ F_CPU */ // Starts the PWM
}
void init_timer(void) /* Setting Timer 0 for trigger every 50us */
{
sei(); // Enable global interrupts
TIMSK |= (1 << OCIE0); // Enable Compare Match interrupt
/*
* Pre-scaled clock = F_CPU / PRESCALAR
* => Each timer counter increment takes PRESCALAR / F_CPU seconds
* => Formula for timer expiry interval is:
* OCR0 (top timer count) * PRESCALAR / F_CPU
* Example: For F_CPU = 8MHz, PRESCALAR = 8
* Pre-scaled clock = 8MHz / 8 = 1MHz
* => Each timer counter increment takes 1/1MHz = 1us
* => Formula for timer expiry interval is OCR0 (top timer count) * 1us
* Example: For 50us = OCR0 * 1us, i.e. OCR0 = 50
*/
OCR0 = (F_CPU / PRESCALAR) / 20000; /* 1/20000 for 50us */
/*
* Setting & Starting the Timer/Counter0 in CTC (Clear Timer on Compare)
* (non-PWM) for controlling timer expiry interval, directly by the compare
* register
*/
TCCR0 = (1 << WGM01) | (0 << WGM00) | PRESCALAR_BITS;
}
void init_switch(void)
{
DDRB &= ~0b00000100; // PB2 as input
PORTB |= 0b00000100; // Pull up on PB2
}
int main(void)
{
init_pwm();
init_timer();
init_switch();
while (1)
{
if (!(PINB & (1 << PB2))) // Switch pressed
{
if (++cur_wave_i == ARR_SIZE(waveform))
{
i = 0; // Reset the index inside the waveform
cur_wave_i = 0;
}
}
_delay_ms(20);
}
return 0;
}
Then, Pugs compiled the program as follows (Note the value of F_CPU defined as 8MHz, same as in the previous article):
$ avr-gcc -mmcu=atmega16 -DF_CPU=8000000 -Os waveforms.c -o waveforms.elf
$ avr-objcopy -O ihex waveforms.elf waveforms.hex
And finally, downloaded the waveforms.hex into the ATmega16 with J1 shorted (same as in the previous articles), using the following command:
$ avrdude -c ponyser -P /dev/ttyUSB0 -p m16 -U flash:w:waveforms.hex:i
Note that Pugs have used the same ATmega16, which has been modified for 8MHz internal clock, same as in the previous article, by writing 0xE4 into the lfuse, using avrdude. Otherwise, you may have to issue the following command as well:
$ avrdude -c ponyser -P /dev/ttyUSB0 -p m16 -U lfuse:w:0xE4:m
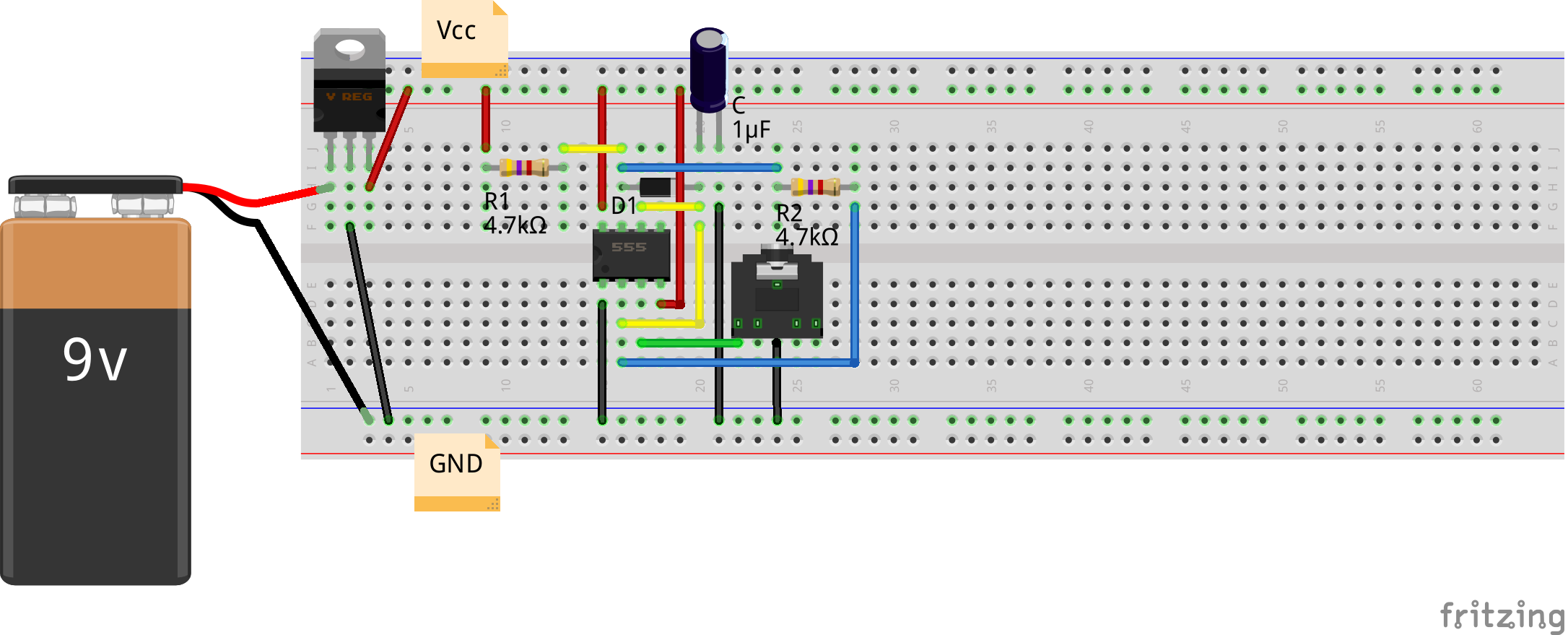
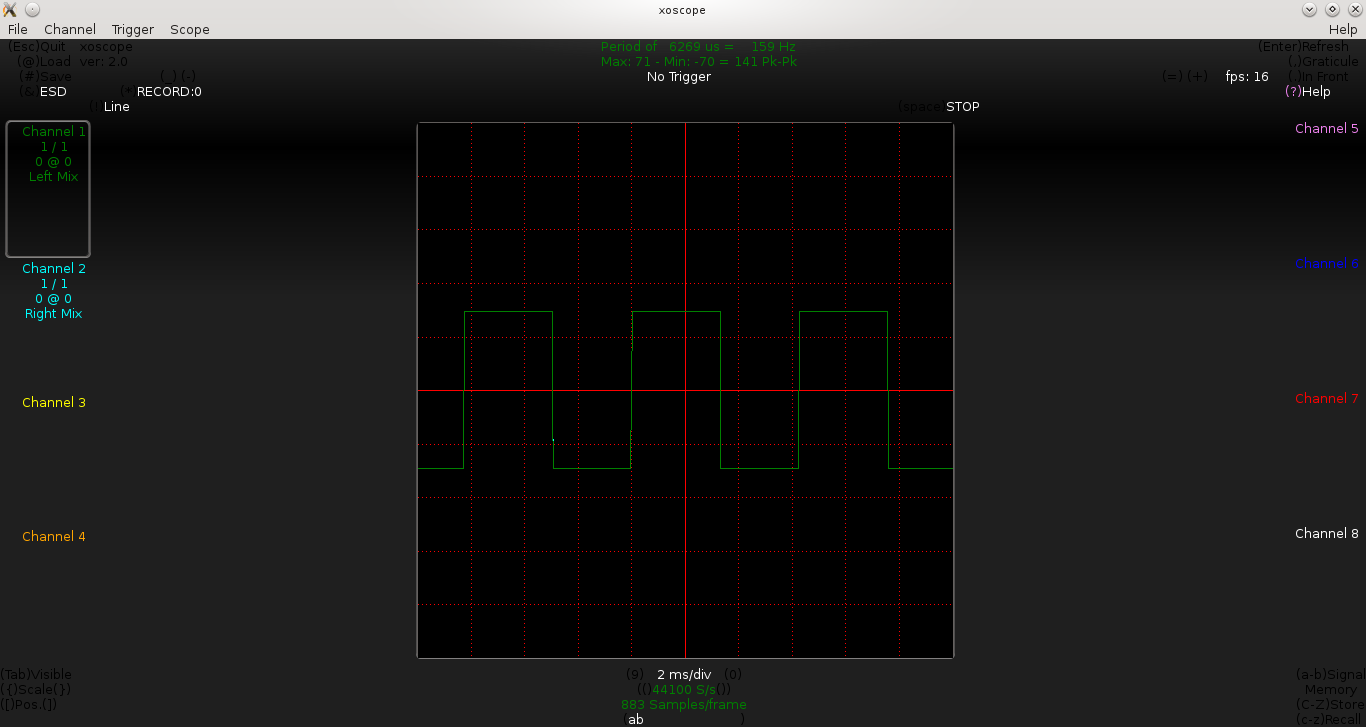
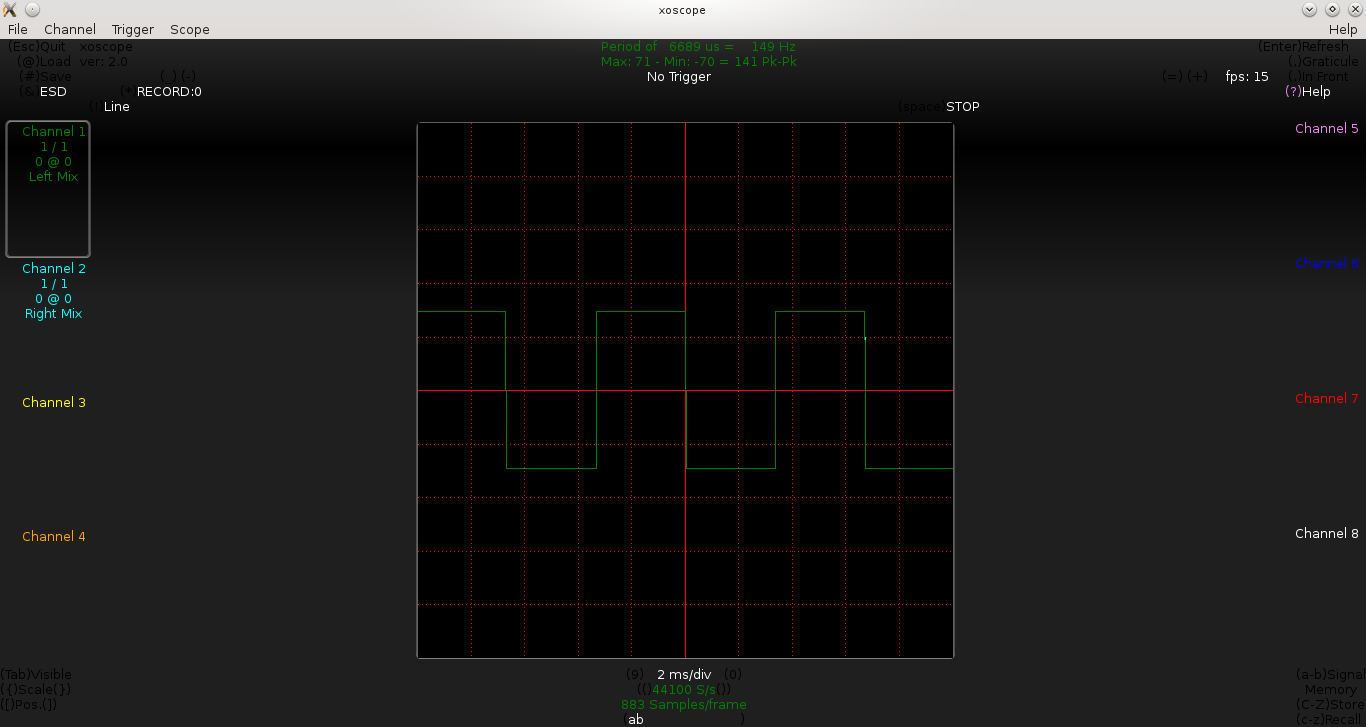
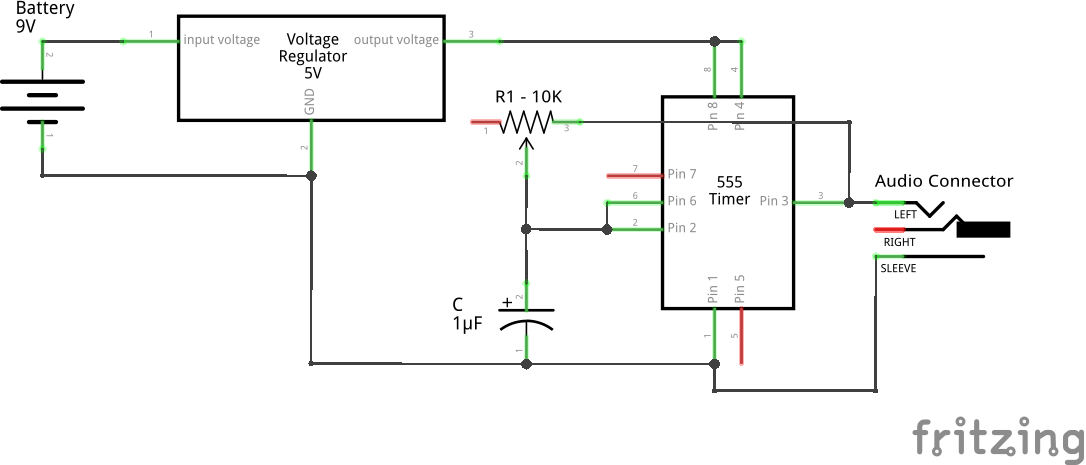
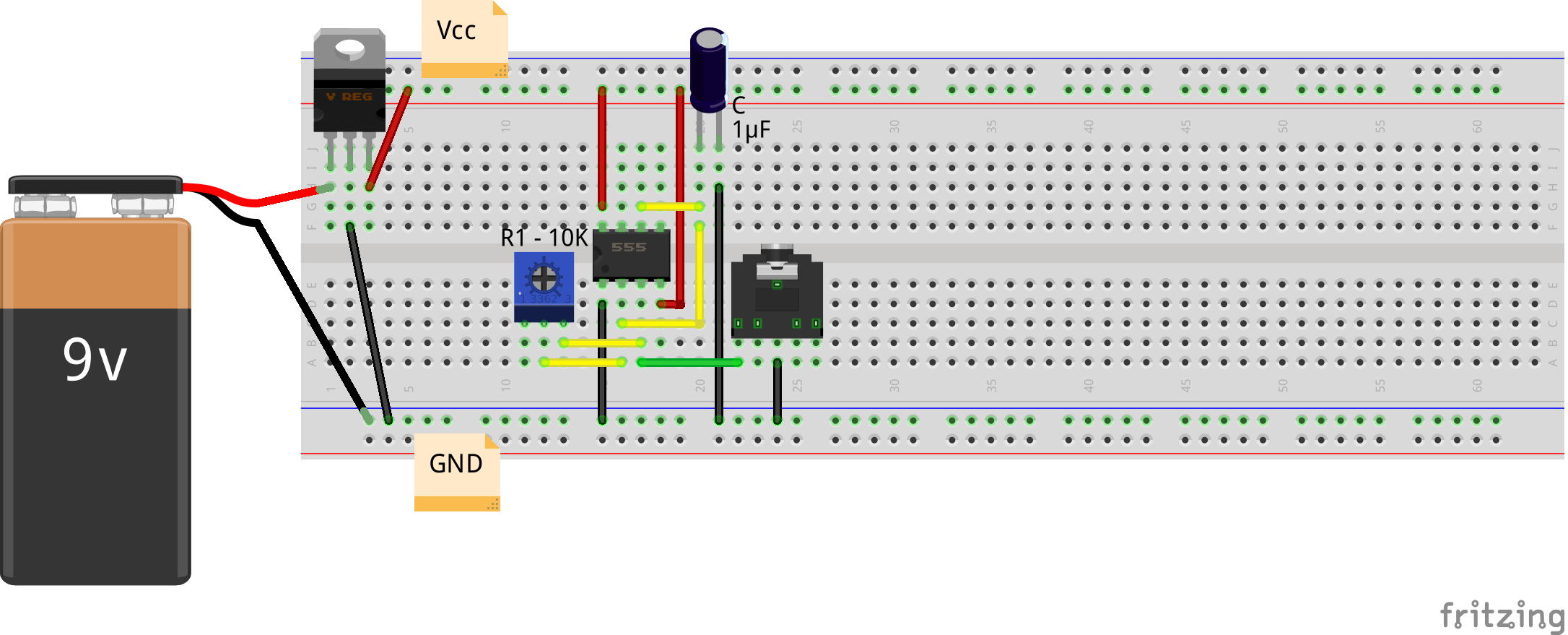
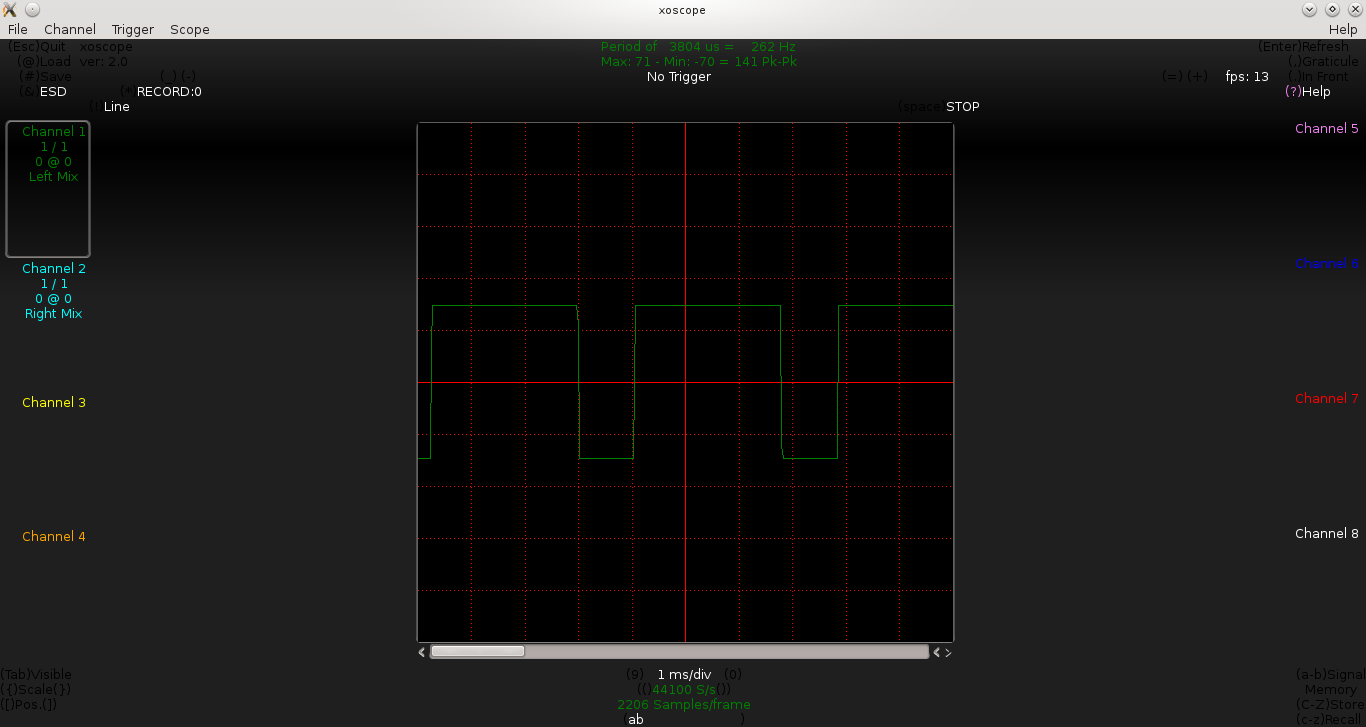
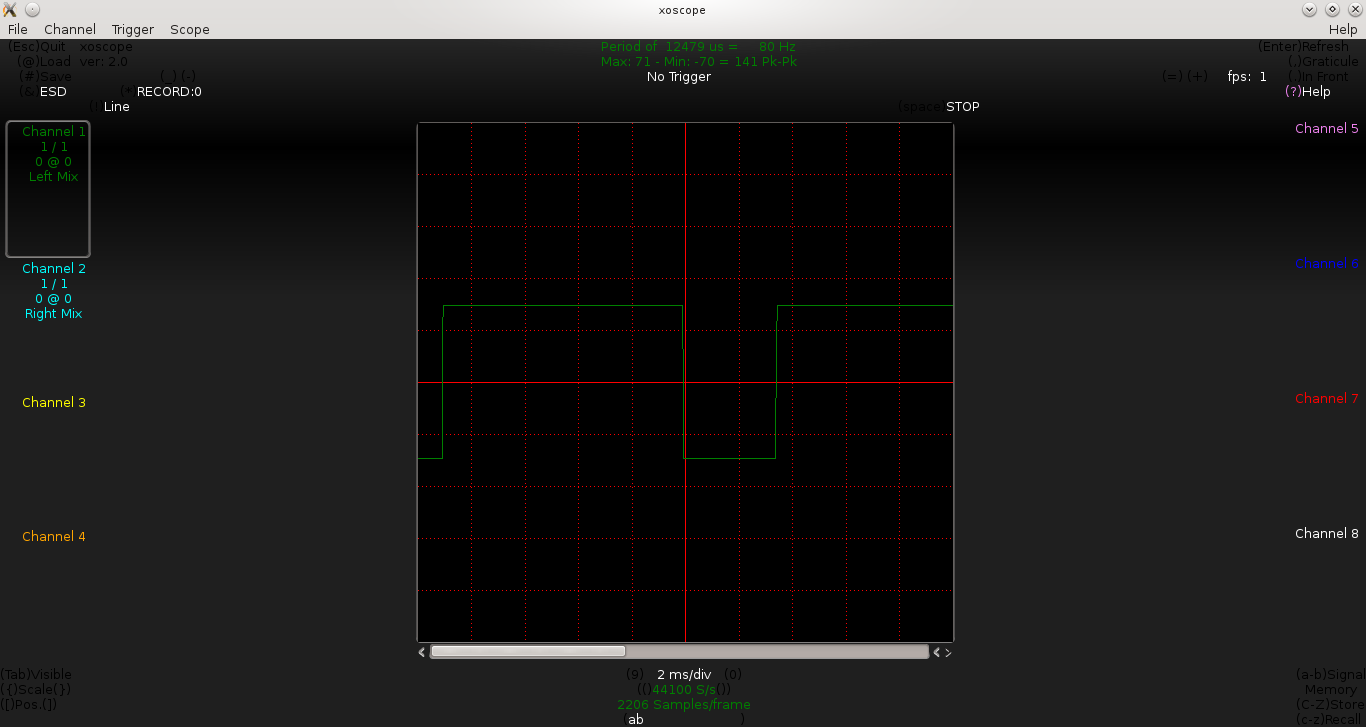
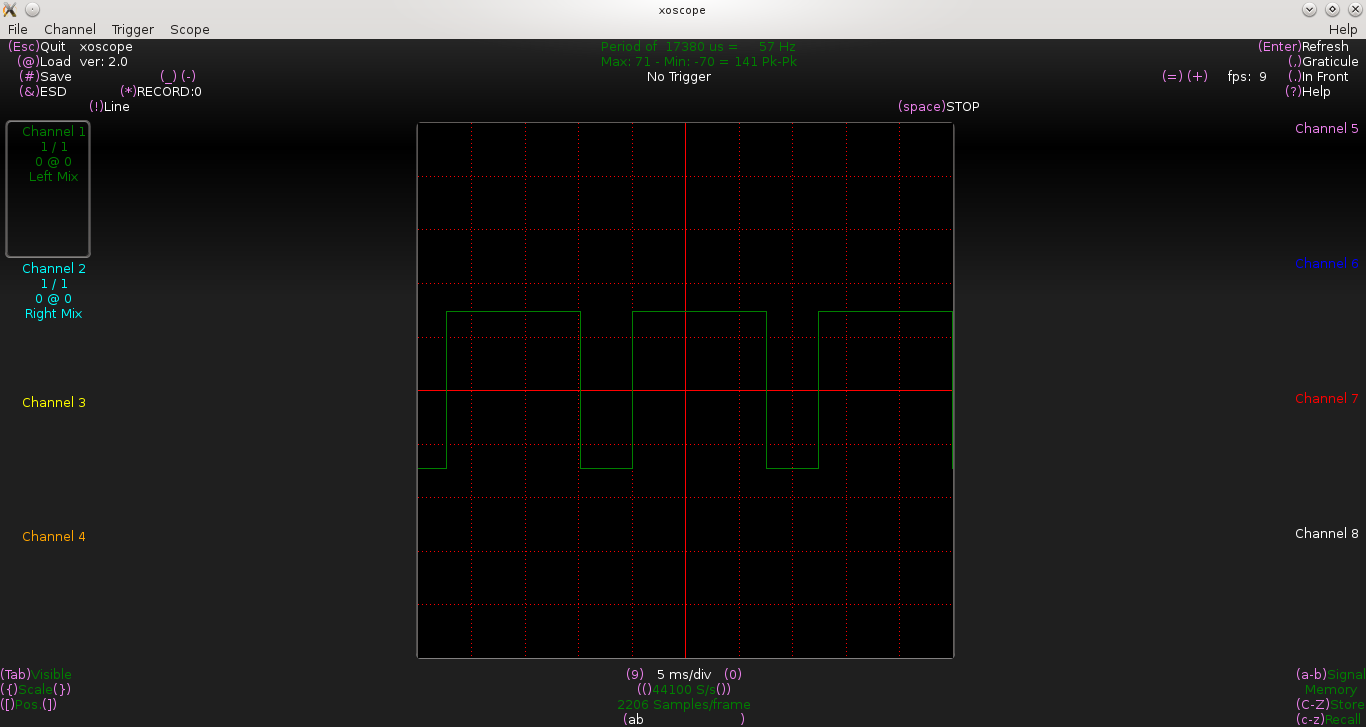
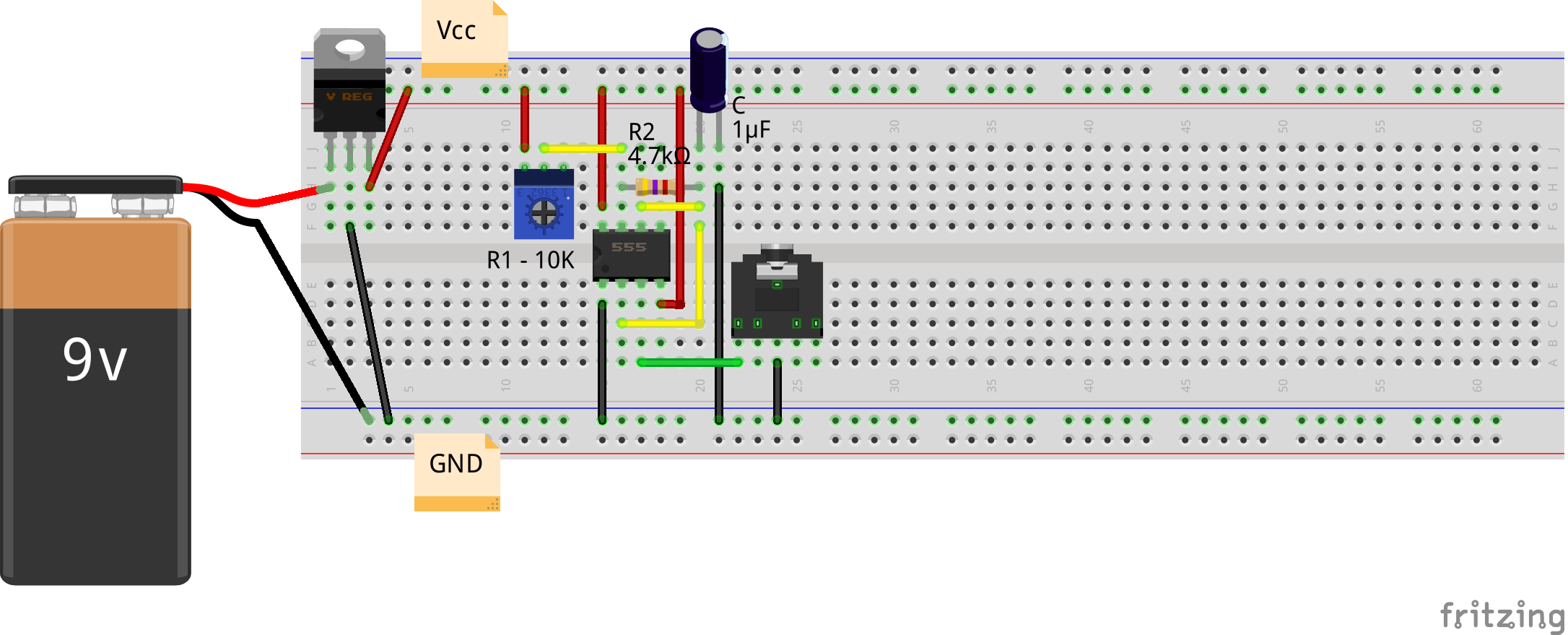
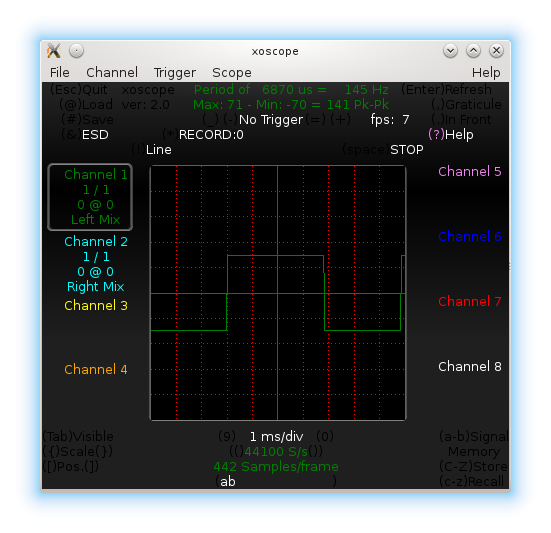
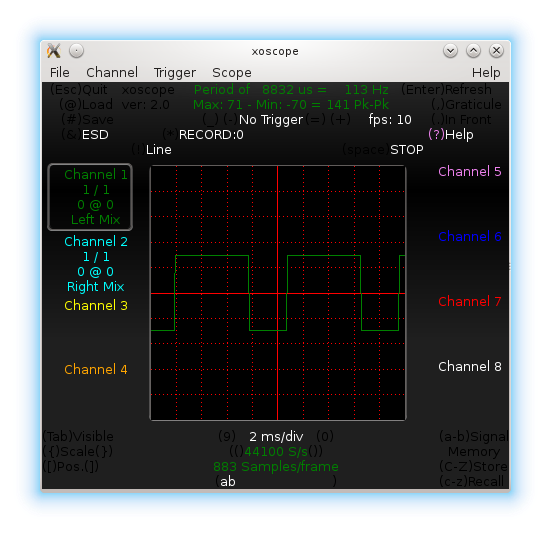
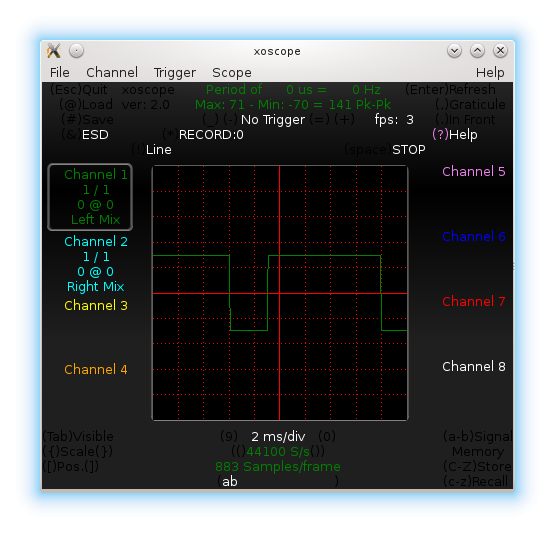
Pugs then checked the output between PD7 and GND pins of the micro-controller (after removing the short of jumper J1), on the home-made PC oscilloscope, as created in his previous PC Oscilloscope article. It showed up the sine wave exactly in the previous article. On press of the switch connected between PB2 and GND, Pugs enjoyed observing the triangular and ramp waveforms of 1 & 2 KHz, as well.
Next Article >>