This is the third article in the series dedicated to the world of Embedded Systems.
“Shall we meet now to further our discussion?” was a text on Pugs’ mobile.
“Where?”, asked Pugs.
“Office Park”, was the reply back from Shweta.
I’ll be there in another 5 minutes.
In the park, “No-thanks, for your time”, were the first words from Pugs.
You won’t change.
Do you want me to?
“Let’s come to the topic – toolchain”, was a change of topic from Shweta, while opening her laptop. “So, your question was, why different toolchains, for different embedded types (BS or OS based), even if they are for same architecture”, she continued.
Wow! You remember my doubt.
Now, to understand that, let me first tell you a bit about the nomenclature (naming conventions) of the toolchain prefix. A native toolchain will have commands like gcc, as, ld, objdump, etc. However, as soon as it is a cross toolchain, a cross compile prefix is prefixed with all these commands as <prefix>-gcc, <prefix>-as, <prefix>-ld, <prefix>-objdump, etc
Yes Yes. I know, e.g. arm-linux-gnueabihf- is prefixed to provide commands like arm-linux-gnueabihf-gcc, arm-linux-gnueabihf-as, etc.
Yes. But the prefix is not random, it is derived based on some naming convention.
O really! What is it?
The prefix is typically created using the following format: <arch>-<vendor>-<os>-<abi>-, where <arch> represents the architecture for which the toolchain would generate the code, <vendor> would be the vendor who created the toolchain, <os> would be the operating system for which the toolchain creates the executable, <abi> denotes the application binary interface (ABI).
What is this application binary interface?
It is an understanding or protocol of interfacing / communicating between the C code (application), and the assembly / machine code (binary). As examples of this protocol, in which CPU register or how in stack would the corresponding parameters of a C function would be placed, where would the return value of a function be placed, floating point computations would be hardware based or in software, etc.
Okay. So, you mean to say, depending on the toolchain, this understanding may also change.
Yes. That’s why, you typically need to compile all software used together with the same toolchain. Examples of ABI are Embedded ABI (EABI), GNU’s EABI (gnueabi), GNU, ELF, etc. And if they incorporate hardware based floating point operations, an “hf” may be suffixed, e.g. gnueabihf.
Hmmm. Examples of <arch> in the prefix would be arm, aarch64, armv8l, etc, right?
Yes. And <os> could be linux or none, if it is for baremetal.
<vendor> could be linaro, right?
Yes. However, in the prefix, many a times the <vendor> is omitted. And even <os> could be omitted if it is none.
Wonderful. So, just by observing the prefix of the commands in a cross toolchain, we can deduce many things about it.
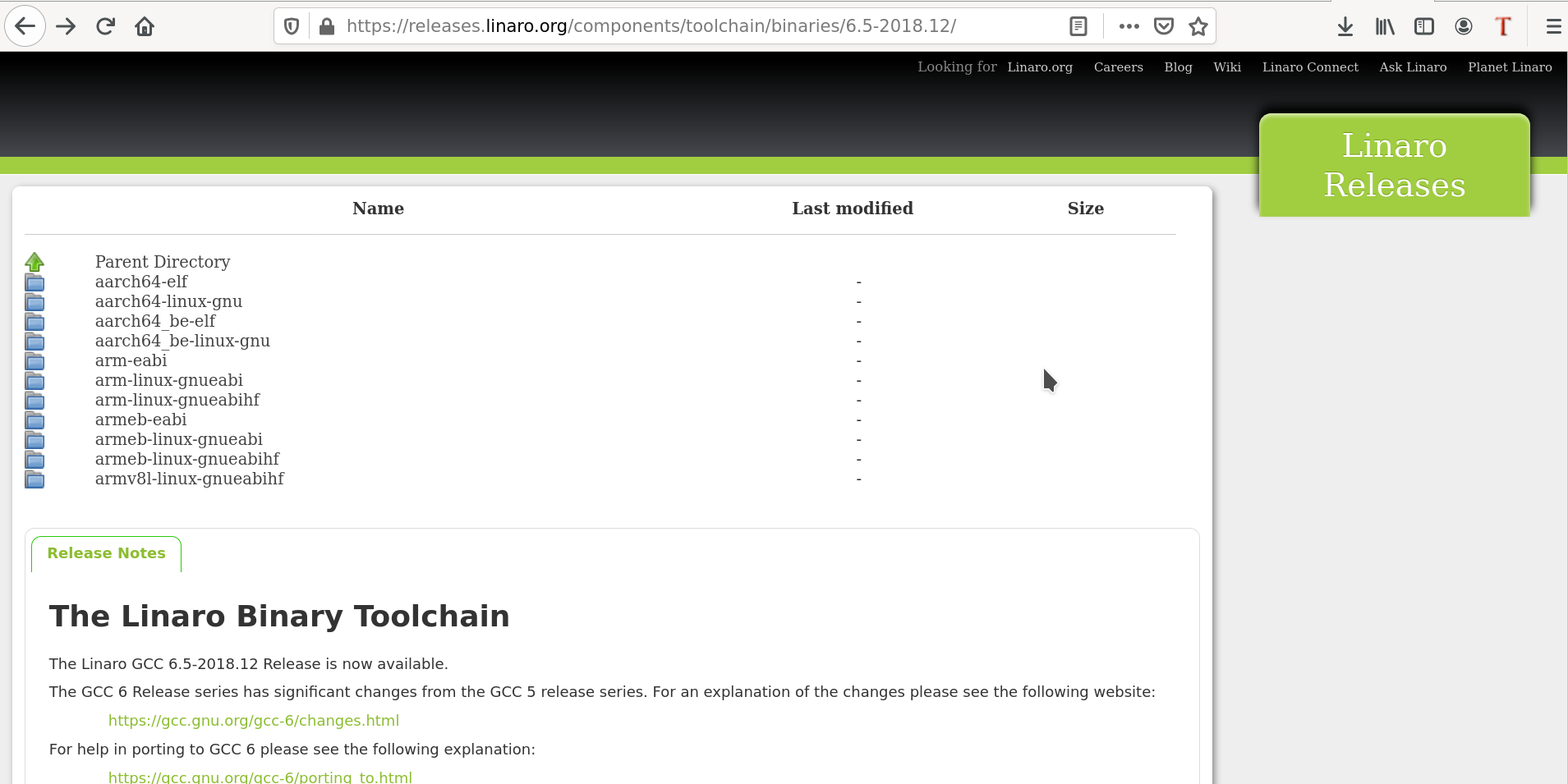
Yes. Just check out some examples here: https://releases.linaro.org/components/toolchain/binaries.
There are so many versions here. Which one?
Say 6.5-2018.12. So, go to: https://releases.linaro.org/components/toolchain/binaries/6.5-2018.12, and you’ll see the following:
Yes. I see there are 3 ARM related toolchains. arm-eabi must be for baremetal, and arm-linux-gnueabi* are for Linux based builds – one with soft float and one with hard float gnueabi.
Excellent. Now, each one of them is available for various host systems – systems where we are going to run the toolchain. As my system is a 64-bit Linux system, I’ll download & install the corresponding arm-eabi and arm-linux-gnueabihf toolchains. One may choose other options in case of different host systems.
Why did you choose two toolchains?
You only wanted, to understand why two different toolchains for the BS and OS based embedded systems, right? So, I’ll setup both and then show you the differences by experimenting with them. And that would answer your question.
Okay. Okay. But, these are tar files, right? How to install?
Just untar them, say under /opt, as follows:
$ sudo tar -C /opt -xf gcc-linaro-6.5.0-2018.12-x86_64_arm-eabi.tar.xz $ sudo tar -C /opt -xf gcc-linaro-6.5.0-2018.12-x86_64_arm-linux-gnueabihf.tar.xz
And then add their executables’ paths in the PATH variable, by adding the following lines in ~/.profile or ~/.bash_profile (as appropriate):
export PATH=~/GIT/bbb-builds/Downloads/gcc-linaro-6.5.0-2018.12-x86_64_arm-eabi/bin:${PATH}
export PATH=~/GIT/bbb-builds/Downloads/gcc-linaro-6.5.0-2018.12-x86_64_arm-linux-gnueabihf/bin:${PATH}
I guess in debian based systems like Ubuntu, we need to add in ~/.profile, and in other rpm based systems in ~/.bash_profile.
Typically, yes.
But these profile files get sourced only when we login, right?
Yes. And so, now after doing the above, I am logging out.
With that Shweta does a logout in her laptop, and then does a login back.
“Now see, the various commands are available on the konsole”, Shweta continued, while showing her screen, after typing arm- and pressing the tab key on her konsole:
Good. Now, like I use gcc and other commands, I can just use these instead.
Yes. With this, we are all set to use the two toolchains, which I’ll use on a simple C program to demonstrate you the differences between the two toolchains, which will clarify “why two”. Meanwhile, why don’t you get your laptop and set it up, to explore alongwith me.
O Yes! That’s a good idea. Let me get it.
With that, Pugs’ goes to fetch his laptop.