This fourteenth article of the mathematical journey through open source, introduces to doing algebra using Maxima.
Maxima is a computer algebra system derived from the earlier Macsyma, which in turn, was written in Lisp.
Algebraic capability of Maxima is the one, which puts it apart from the others. We have worked through basic shell maths, bench calculator bc, and finally the ultra capable octave. But none of them could do algebra with symbols, also referred as symbolic or analytic mathematics. Let’s walk through a few examples to demonstrate what it means.
Getting started
Maxima command line can be started on the shell by typing maxima. -q option to it suppresses the initial welcome message. Typing quit(); on the Maxima command line quits Maxima. Typical Maxima commands shall be terminated either with a semicolon (;) or a dollar ($) – the later suppressing any print from the command. Outputs are numbered and prefaced by %o. Inputs are also numbered, and prefaced by %i. Here are a few factorization examples:
$ maxima -q
(%i1) factor(x^3 - 1);
2
(%o1) (x - 1) (x + x + 1)
(%i2) factor((x + 1)^4);
4
(%o2) (x + 1)
(%i3) expand(%o2);
4 3 2
(%o3) x + 4 x + 6 x + 4 x + 1
(%i4) factor(6!);
4 2
(%o4) 2 3 5
(%i5) expand(6!);
(%o5) 720
(%i6) quit();
factor() and expand() are two complementary functions doing factorization & simplification, respectively. Note the way the powers in the output are printed. For example, 6! is factorized as 24 * 32 * 5. In case, we want the output on a single line, we may use the command string(), which we shall use now onwards. Also, note the usage of output labels as inputs to the commands, namely expand(%o2) in the above example.
Integration and differentiation
Octave has enabled us to do integration and differentiation, but more of definite integrals and differences. Yes, it has indefinite operations for polynomials. But with Maxima, we can just plug in the expressions, as we usually do on our maths notebooks. This is what it means:
$ maxima -q
(%i1) integrate(cos(x),x);
(%o1) sin(x)
(%i2) diff(cos(x),x);
(%o2) - sin(x)
(%i3) string(integrate(1/(a^2 + x^2)^(3/2),x));
(%o3) x/(a^2*sqrt(x^2+a^2))
(%i4) string(diff(log(x), x));
(%o4) 1/x
(%i5) y: (x+1)^2$ /* $ suppresses the output */
(%i6) string(diff(y, x));
(%o6) 2*(x+1)
(%i7) string(integrate(y, x));
(%o7) x^3/3+x^2+x
(%i8) quit();
Variable assignments can be done in Maxima using colon (:), as shown in the input %i5, above. There onwards, the variable can be used instead of the original expression, as shown in the inputs %i6 & %i7. Note that the variable assignment assigns the complete symbolic expression, unlike the usual value assignments.
Solving equations
Whether it be linear set of equations, polynomial equations, or for that matter non-linear equations, Maxima can solve most of them with quite ease, and that also in a analytical way. Here are a few common examples: 1) The two solutions of a quadratic equation; 2) Two simultaneous equations in two variables; 3) A non-linear equation with irrational number e. Maxima code demonstration follows:
$ maxima -q
(%i1) string(solve(a*x^2 + b*x + c = 0, x));
(%o1) [x = -(sqrt(b^2-4*a*c)+b)/(2*a),x = (sqrt(b^2-4*a*c)-b)/(2*a)]
(%i2) string(solve([a*x + b*y = c,d*x + e*y = f],[x, y]));
(%o2) [[x = -(c*e-b*f)/(b*d-a*e),y = (c*d-a*f)/(b*d-a*e)]]
(%i3) string(solve([exp(x) + 1/exp(x) = a],[x]));
(%o3) [x = log(a/2-sqrt(a^2-4)/2),x = log(sqrt(a^2-4)/2+a/2)]
(%i8) quit();
Equation solving has been one of the most fascinating as well as challenging tasks for solving mathematical problems, since ages. So, when the computer is there to aid it, we try to go beyond the human limitations. We just saw the well-known formula for the two solutions of a quadratic equation. How about the same for a cubic equation? It looks really complicated and hence we typically don’t use it. But, still you want to see it. Here it goes:
$ maxima -q
(%i1) string(solve(a*x^3 + b*x^2 + c*x + d = 0, x));
(%o1) [x = (-sqrt(3)*%i/2-1/2)*(sqrt(27*a^2*d^2+(4*b^3-18*a*b*c)*d+4*a*c^3-b^2*c^2)/
(2*3^(3/2)*a^2)-(27*a^2*d-9*a*b*c+2*b^3)/(54*a^3))^(1/3)-(sqrt(3)*%i/2-1/2)*(3*a*c-
b^2)/(9*a^2*(sqrt(27*a^2*d^2+(4*b^3-18*a*b*c)*d+4*a*c^3-b^2*c^2)/(2*3^(3/2)*a^2)-
(27*a^2*d-9*a*b*c+2*b^3)/(54*a^3))^(1/3))-b/(3*a),x = (sqrt(3)*%i/2-1/2)*(sqrt(27*
a^2*d^2+(4*b^3-18*a*b*c)*d+4*a*c^3-b^2*c^2)/(2*3^(3/2)*a^2)-(27*a^2*d-9*a*b*c+2*b^3)/
(54*a^3))^(1/3)-(-sqrt(3)*%i/2-1/2)*(3*a*c-b^2)/(9*a^2*(sqrt(27*a^2*d^2+(4*b^3-18*a*
b*c)*d+4*a*c^3-b^2*c^2)/(2*3^(3/2)*a^2)-(27*a^2*d-9*a*b*c+2*b^3)/(54*a^3))^(1/3))-b/
(3*a),x = (sqrt(27*a^2*d^2+(4*b^3-18*a*b*c)*d+4*a*c^3-b^2*c^2)/(2*3^(3/2)*a^2)-(27*
a^2*d-9*a*b*c+2*b^3)/(54*a^3))^(1/3)-(3*a*c-b^2)/(9*a^2*(sqrt(27*a^2*d^2+(4*b^3-18*
a*b*c)*d+4*a*c^3-b^2*c^2)/(2*3^(3/2)*a^2)-(27*a^2*d-9*a*b*c+2*b^3)/(54*a^3))^(1/3))-
b/(3*a)]
(%i2) quit();
And that’s what is the power of Maxima.
Plotting graphs
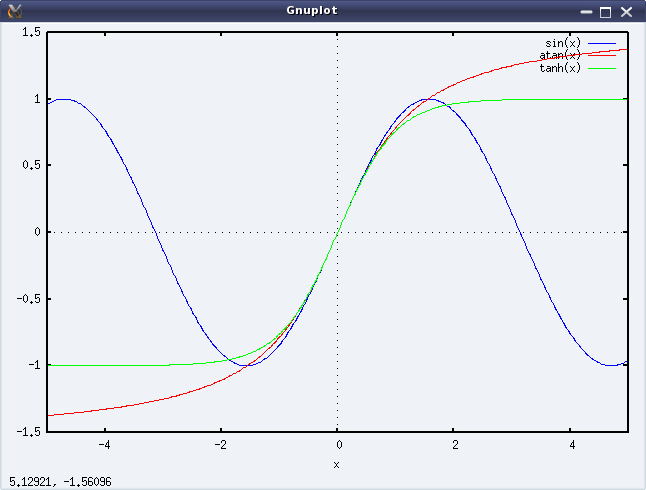
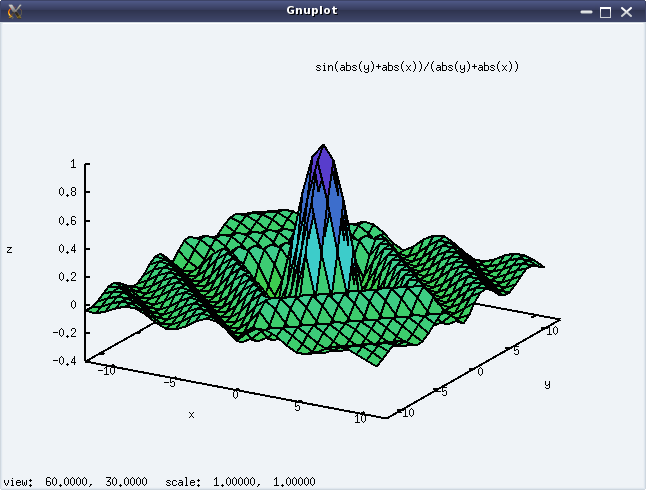
Along with the algebraic processing, Maxima also supports graph plotting for the algebraic expressions, though we must specify the intervals to plot it. It can do 2-D as well as 3-D plots. The following code shows an example for each of these. And figures 22 & 23 show the respective plots.
$ maxima -q
(%i1) plot2d([sin(x), atan(x), tanh(x)], [x, -5, 5])$
(%i2) plot3d(sin(abs(x) + abs(y))/(abs(x) + abs(y)),[x, -12, 12], [y, -12, 12])$
(%i3) quit();
After this first glimpse of what Maxima can do, we are now ready to move on to detail out the specific topics, like expression simplification, polynomials, etc.









Pingback: Octavian Statistics | Playing with Systems
Pingback: Expression Simplification using Maxima | Playing with Systems
I have not found anything on Algebraic simplification for adding expressions to equations in Maxima.
Like x+a=2b^2 become x+a+b=2b^2+b by adding b on both sides. This way we can transpose terms within equations. Hoping to get your help,
Do you need to add this yourself? Then, just add it. Otherwise, when do you expect maxima to automatically add it?